
![]() Water and
global warming
Water and
global warming![]() Absorption spectra of
gaseous, liquid and solid water
Absorption spectra of
gaseous, liquid and solid water![]() The vibrational spectra of
liquid water
The vibrational spectra of
liquid water![]() The visible and UV spectra of
liquid water
The visible and UV spectra of
liquid water
Water is the main absorber of the sunlight in the atmosphere. The 13 million million tons of water in the atmosphere (~0.33% by weight) is responsible for about 70% of all atmospheric absorption of radiation, mainly in the infrared region where water shows strong absorption. It contributes significantly to the greenhouse effect ensuring a warm habitable planet, but operates a negative feedback effect, due to cloud formation reflecting the sunlight away, to attenuate global warming. The water content of the atmosphere varies about 100-fold between the hot and humid tropics and the cold and dry polar ice deserts.
The water absorption spectrum is very complex. Water's vapor spectroscopy has been recently reviewed [348]. The water molecule may vibrate in a number of ways. In the gas state, the vibrations [607] involve combinations of symmetric stretch (v1), asymmetric stretch (v3) and bending (v2) of the covalent bonds with absorption intensity (H216O) v1;v2;v3 = 0.07;1.47;1.00 [8]. The stretch vibrations of HD16O refer to the single bond vibrations, not the combined movements of both bonds.
|
Gas |
v1,
cm-1 |
v2,
cm-1 |
v3,
cm-1 |
|---|---|---|---|
|
H216O |
3657.05 |
1594.75 |
3755.93 |
|
H217O |
3653.15 |
1591.32 |
3748.32 |
|
H218O |
3649.69 |
1588.26 |
3741.57 |
|
HD16O |
2723.68 |
1403.48 |
3707.47 |
|
D216O |
2669.40 |
1178.38 |
2787.92 |
|
T216O |
2233.9 |
995.37 |
2366.61 |
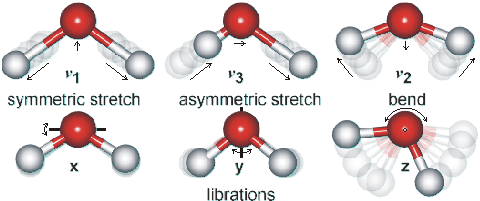
Shown opposite are the main vibrations occurring in water. The movements are animated using the cursor. The dipole moments change in the direction of the movement of the oxygen atoms as shown by the arrows. As the H-atoms are light, the vibrations have large amplitudes.
The water molecule has a very small moment of inertia on rotation which gives rise to rich combined vibrational-rotational spectra in the vapor containing tens of thousands to millions of absorption lines. In the liquid, rotations tend to be restricted by hydrogen bonds, giving the librations. Also, spectral lines are broader causing overlap of many of the absorption peaks.
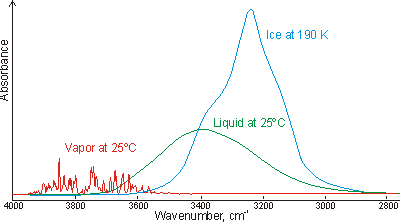
Opposite is shown a comparison of the gas, liquid and solid spectra of the same amount of H2O [1392].
The main stretching band in liquid water is shifted to a lower
frequency (v3, 3490 cm-1 and
v1, 3280 cm-1 [8]) and the bending
frequency increased (v2, 1644 cm-1 [942]) by hydrogen bonding. As seen,
increased strength of hydrogen bonding typically shifts the stretch vibration to
lower frequencies (red-shift) with greatly increased intensity in the infrared
(but not Raman) due to the increased dipoles. Blue-shifting hydrogen bonds are
described elsewhere.
[Back to
Top ![]() ]
]
|
Vibration(s) [942]
|
liquid H2O (25°C) |
liquid D2O (25°C)
| ||
|---|---|---|---|---|
|
v, cm-1 |
E0, M-1
cm-1 |
v, cm-1 |
E0, M-1
cm-1 | |
| v2 |
1643.5 |
21.65 |
1209.4 |
17.10 |
| combination of v2+ libration |
2127.5 |
3.46 |
1555.0 |
1.88 |
| v1, v3 , and overtone of v2 |
3404.0e |
100.61 |
2504.0 |
69.68 |
Variations in the environment around each liquid water molecule gives rise to considerable line broadening with vibration shifts in a hydrogen-bond-donating water molecule being greater than in a hydrogen-bond accepting molecule but both acting in the same direction [679], and accumulating with the number of hydrogen bonds. The strength of the hydrogen bonding depends on the cooperative/anticooperative nature of the surrounding hydrogen bonds with strongest hydrogen bonds giving the lowest vibrational frequencies [852]. Stretching frequency increases about 360 (at 3.1 Å) -1000 (at 2.6 Å) cm-1Å-1 with increasing O····O distance and about 9 cm-1 degree-1 with increasing O-H····O bend [446]. The absorption intensity of these bands is v1;v2;v3 = 0.87;0.33;1.00 [8]. In supercooled water, the spectra is shifted to lower frequency with a 70 cm-1 shift of the stretch frequency and 30% increase in its intensity between 298 K and 238 K [1065]. Ultimately a stretch peak at 3120 cm-1 dominates, as it also does in amorphous ice ( LDA) [1252]. In hexagonal ice, these bands are shifted further (v1, 3085 cm-1, v2, 1650 cm-1,v3, 3220 cm-1).
In liquid water the molecular stretch vibrations shift to higher frequency, on raising the temperature (as hydrogen bonding weakens, the covalent O-H bonds strengthen causing them to vibrate at higher frequencies) whereas the intramolecular vibrations shift to lower frequencies and the molecular bend vibration peak shifts to lower frequencies and becomes both narrower [696] and stronger. These differences between stretch and bend vibrations are due to the increased importance of intramolecular hydrogen bonding at lower temperatures that tends to reduce intra-molecular bending whilst encouraging stretching. Thus in the extreme non-hydrogen bonded state, the 'dangling' O-H bond stretch frequency at surfaces where the water molecule has three hydrogen bonds (two accepting and one donating) is at 3697 cm-1 [1246]. Raising the temperature also lowers the intensity of the stretching bands. This divergent behavior of bending and stretching vibrations allows their contributions to combination bands to be discerned. Thus, combinations of stretching vibrations shift to higher frequency with temperature with this trend reduced when bending vibrations are also combined. As examples, the first overtone combination of symmetric and asymmetric stretching shows a shift from strongly hydrogen-bonded structures (6707 cm-1) to weakly hydrogen bonded structures (7082 cm-1) with increasing temperature [237], and the combination band at about 5200 cm-1 shifts to slightly higher wavenumbers with reduced hydrogen bond strength [282].
The second overtone of the stretching band gives rise to a significant peak in the near-infrared spectrum (λ 970 nm). Recent work shows that the intensity of all overtone bands tend to increase linearly with increasing temperature in the range 2°C - 85°C without isobestic points (in contrast to earlier reports [530]), so ruling out a simple two-phase model for water [526]. However IR evanescent wave spectroscopy does show isobestic points in the O-H stretch region [699]. These apparently confused conclusions may be more supportive of progressively changing two-phase models such as described here. Increasing the pressure on water decreases the O····O distances (graphed elsewhere) so increasing the covalent O-H distances and lowering their stretch frequency [804]. Raised pressure also causes a reduction in long, weak or broken bonds and an increase in bent and short, strong hydrogen bonds [804].
The overtone bands of water (~1100 nm - 2500 nm, in a scientific discipline known as AquaPhotomics) have been shown to be good discriminatory, and non-destructive, indicators of changes in aqueous structuring in disease diagnosis and protein conformation and have aided the understanding of the role of water in biological systems [1615a]. A database of such interactions is being built up [1615b].
The spectra for isotopic variants of water (for example, HDO, D2O and H218O) are all different; in particular the H-O (~3400 cm-1) and D-O (~2500 cm-1) stretching vibrations are not connected in HDO but the related vibrations in H2O and D2O involve both hydrogen atoms.
|
Wavelength |
cm-1 |
Assignment |
Wavelength** |
cm-1 |
Assignment | |
|---|---|---|---|---|---|---|
| 0.2 mm | 50 | intermolecular bend | 1470 nm | 6800 | av1 + bv3; a+b=2 | |
| 55 μm | 183.4 | intermolecular stretch | 1200 nm | 8330 | av1 + v2 + bv3; a+b=2 | |
| 25 μm | 395.5 | L1, librations | 970 nm | 10310 | av1 + bv3; a+b=3 | |
| 15 μm | 686.3 | L2, librations | 836 nm | 11960 | av1 + v2 + bv3; a+b=3 | |
| 6.08 μm | 1645 | v2, bend | 739 nm | 13530 | av1 + bv3; a+b=4 | |
| 4.65 μm | 2150 | v2 + L2 b | 660 nm | 15150 | av1 + v2 + bv3; a+b=4 | |
| 3.05 μm | 3277 | v1, symmetric stretch | 606 nm | 16500 | av1 + bv3; a+b=5 [526] | |
| 2.87 μm | 3490 | v3, asymmetric stretch | 514 nm | 19460 | av1 + bv3; a+b=6 [526] | |
| 1900 nm | 5260 | av1 + v2 + bv3; a+b=1 |
Note that a and b are integers, ≥ 0
ms. | |||
* Raman peaks are given in [805].
**Wavelength (nm) =
107/wavenumber (cm-1) (nm ~3.3
attosecond)
The near-infrared (NIR) bands (at about λ 970-1940 nm) are suited
to rapid non-destructive water determination [479], all shifting a few nm to longer wavelength (lower frequency)
with strengthening hydrogen bonding due to shifts from high density water (that
is, increasing CS) to low density water (that is, increasing ES) [489]. A shoulder at about 3250 cm-1 on the side of the
only strongly active Raman peak, and recently described in the IR spectrum at
3220 cm-1 [699], (symmetric O-H
stretch, v1) of liquid water has been assigned to the
collective in-phase symmetric O-H vibrations of strongly tetrahedrally-bonded
water patches. The ratio of this to the remaining peak at about 3400
cm-1 has been used to determine the fraction of such water but such
comparisons, although commonly used, should be treated with caution, as their
absorbencies are unlikely to be identical and other possible vibrations, such as
the first bend (v2) overtone, will interfere. This remaining
peak has been analyzed in many ways (for example, as zero, single, double and
triple coordinated hydrogen-bonded water) but most convincingly in terms of
three-coordinate (double acceptor single donor, 3400 cm-1; single
acceptor double donor, 3535 cm-1) and two-coordinate (single acceptor
single donor, 3630 cm-1) hydrogen-bonded water molecules [699]. There is clearly
much structural information hidden in the vibrational spectra of water, if only
it can be unambiguously interpreted (see methods page). Some
success has recently been made using femtosecond mid-infrared nonlinear
spectroscopy [189, 190] and the theoretical Raman spectra of water clusters [483]. ![]()
In liquid water and ice the infrared and Raman spectra are far more complex than the vapor due to vibrational overtones and combinations with librations (restricted rotations; that is, rocking motions). These librations are due to the restrictions imposed by hydrogen bonding (minor L1 band 395.5 cm-1; major L2 band 686.3 cm-1; both for liquid water at 0°C, the absorbance of L1 increasing with increasing temperature whereas L2 absorbance decreases but broadens with reduced wavenumber with increasing temperature [177]). Ice has a sharper major band at 819 cm-1 (-10°C) with a very minor band at about 510 cm-1 [1219]. The librations depend on the moments of inertia such that the almost doubling of the moments of inertia of D2O, relative to H2O, reduces the frequencies by about a factor of √2. Cluster vibrations such as translational vibrations involve combinations of hydrogen bond O-H····O stretching and bending at around 200 cm-1 (6 THz) [ 240] (S or connectivity band, 183.4 cm-1 (5.5 THz); at 0°C, the hydrogen bond stretch absorbance increasing with decreasing temperature [819]a; with a major sharp band at 215 cm-1 (6.4 THz) and a minor sharp band at 155 cm-1 (4.6 THz) in ice Ih at -10°C [1219]. These involve hydrogen-bonded network movements along linear or near-linear hydrogen bonds and show relatively small differences between H2O and D2O, due to their slightly different masses [1004]. The Raman spectrum also involves an overlapping band involving the reorienting of the molecular dipoles around the hydrogen bonds [1384]. Some report bending vibrations of the hydrogen bonds also occur, due to out of alignment translations relative to the hydrogen bonds (B band ~40 - 60 cm-1 (1.2-1.8 THz); at 0°C, the absorbance increasing with temperature [608]) [1004]. It seems likely that this 60 cm-1 peak is strongly localized within a local cluster and not connected with the more extensive hydrogen-bonded network [1549]. Also in liquid water there is a small but significant combination band (IR and Raman) of the bending (v2) and libration modes at 2125 cm-1 (2270 cm-1 in ice Ih; the 'association band').b
A contribution to the Raman scattering of water at 50 cm-1 (1.5 THz) has been attributed to the low-frequency vibrations of oxygen-oxygen bonds at the vertices of pentagonal dodecahedral structures [165] or simply O····O····O bending motions [901]. Such low-frequency features (centered around 60 cm-1, 1.8 THz) are also observed in the spectra of dense non-associated liquids, such as the noble gases, and may be attributed to non-bonded 'cage effects' where translations are frustrated [448]. This same effect, however, may also operate within hydrogen bonded 'cage effects' consistent with the 60 cm-1 absorption band [900]. Further confirmation of the hydrogen-bonding source for this absorption comes from the use of an intense source of far infrared radiation showing temperature dependent peaks at a number of wavelengths in the 40-90 cm-1 (1.2-2.7 THz) range [656]. The infrared spectrum runs into microwave radiation at longer wavelengths. This interacts with the water dipole, moving the molecules backwards and forwards and so stretching and bending the hydrogen bonds, which generates heat. If the radiation is at too high a frequency (> 1000 GHz, λ < 0.3 mm), the molecules do not have time to react to the electromagnetic field changes and no heat is generated. If the radiation is at lower frequencies (< 1 GHz, λ > 30 cm), the molecules react to the electromagnetic field changes but so slowly that effectively no heat is generated. Pure water is almost totally transparent to such low frequency radiation. The maximum absorption varies to higher frequencies at higher temperatures when the weaker hydrogen bonding allows a quicker response to changes in the field [136]. Microwave ovens typically use radiation at 2.450 GHz (λ 12.24 cm). More details on the response of water to microwave radiation are available on another page.
Anions may be classified as kosmotropes or chaotropes according to how the effect the water's stretch vibrations; ionic kosmotropes (for example, F-) causing broadening and movement to lower wavenumbers whereas chaotropes (for example, I-) causing narrowing and movement to higher wavenumbers [758]. Primarily this seems due to water's ability to hydrogen bond to the anions. The vibrational spectra of H3O2- and H5O2+ are described on another page.
The reported structuring absorption of sound by water is not
generally accepted. [Back to
Top ![]() ]
]
Absorption coefficientsd for water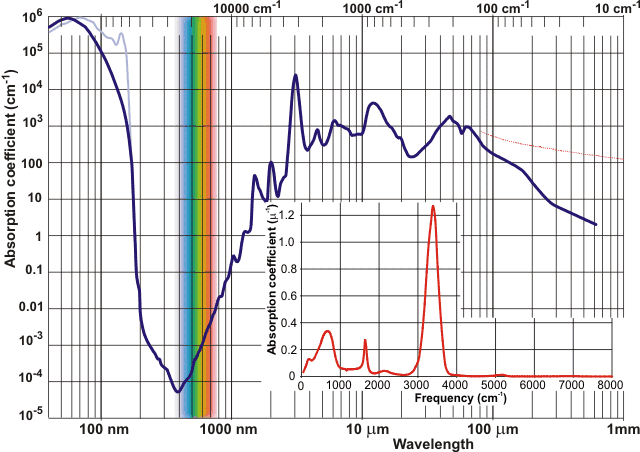
Water is almost perfectly transparent to 'visible' light, a property which is made good use of by photosynthesis and allowing production of both biomass and oxygen. Water is very slightly blue in color [131]c as overtone and combination vibrational absorption bands (albeit far less intense, see above [130]) extend through the red part of the visible spectrum with a small peak at 739 nm and shoulder at 836 nm, both varying somewhat with temperature [268] plus a smaller fourth overtone of the v1:v3 stretch at 606 nm, and very small fifth overtone (at 514 nm) and combined overtone (at 660 nm) bands. This absorption spectrum of water (red light absorbs 100 times more than blue light), together with the five-times greater scattering of blue light over red light, contributes to the blue color of lake, river and ocean waters. Colloidal silica may contribute to the outstanding blue color of certain, often hydrothermal, pools and lakes [372]. Ice is also blue [159] for similar reasons but liquid D2O does not absorb in the red region (as the absorption band is shifted into the infrared) and is blue solely because of the light scattering effect [159].
Although the absorptions of water's overtone bands within the visible spectrum are quite small (~0.3-0.01 m-1), they are sufficient to create spectral niches amongst photosynthetic organisms; thus directing water ecology and evolution [1281].
The first peak in the far UV of gaseous water (166.5 nm [902], shown light blue in the spectrum above) is due
to excitation from the occupied pz2-type molecular 1b1
orbital (interactive orbitals are available, COW only [Plug-in, ActiveX]). Absorption of UV
close-by (~125 nm), excites the 3a1
orbital leading to dissociation into OH + H (photodissociation; higher
energy absorption produces charged fragments [1299]). Such dissociation can also be achieved by consecutive
absorption of two 266 nm photons [589]. Absorption of two higher energy photons, at 200 nm, gives rise
to a hydrated electron by H2O + hν ![]() H2O+ +
e-aq [1057]. Inelastic x-ray scattering studies find this far UV peak to be
absent in liquid water [355], where the
major peak is at about 56 nm. [Back to
Top
H2O+ +
e-aq [1057]. Inelastic x-ray scattering studies find this far UV peak to be
absent in liquid water [355], where the
major peak is at about 56 nm. [Back to
Top ![]() ]
]
a Dielectric studies showed an opposite effect with the absorbance at around 200 cm-1 increasing with increasing temperature to about 30°C before reducing with increasing temperature due to hydrogen bond breakage [608]. The discrepancy may be due to additional relaxation processes detected by these dielectric studies in addition to the hydrogen bond stretching detected by infrared spectroscopy [819]. [Back]
b This band may be due to third overtone of the libration band, with the second overtone introducing asymmetry into the bend (v2) vibration [699b]. The dependence of this band on hydrogen bonding makes it sensitive to changes in liquid and solution structuring, although this importance is seemingly often overlooked. [Back]
c The sky is blue due to molecular light scattering, with neither tiny air-borne particles nor its small and variable content of gaseous water having significant effect [710]. [Back]
d This curve(s) has been
generated using data for liquid and frozen water to give a continuous curve
showing the main features. For exact data please consult the original references
[130]. The absorption
coefficient μa(λ), with units of cm-1, at a particular
wavelength (λ) is given by the equation![]() where I is
the transmitted intensity of the light, I0 is the incident
intensity of the light and l is the path length (cm). The absorbance
(A, in optical density units) is defined by the equation
where I is
the transmitted intensity of the light, I0 is the incident
intensity of the light and l is the path length (cm). The absorbance
(A, in optical density units) is defined by the equation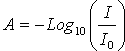 . The transmittance (T) of a sample is defined by
. The transmittance (T) of a sample is defined by 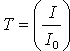 .
The molar extinction coefficient ε(λ), with units liters
mole-1 cm-1, is defined by the equation A=
ε(λ)cl where c is the molar concentration (= 55.345
M for liquid water at 25°C) and l is the path length (cm). Comparison
of these definitions shows that
.
The molar extinction coefficient ε(λ), with units liters
mole-1 cm-1, is defined by the equation A=
ε(λ)cl where c is the molar concentration (= 55.345
M for liquid water at 25°C) and l is the path length (cm). Comparison
of these definitions shows that![]() and
and ![]() (note that loge(10) =
2.302585). [Back]
(note that loge(10) =
2.302585). [Back]
e This band in the Raman spectrum has been clearly separated into three peaks at ~3210, 3450 and 3650 cm-1 [1310]. The two dominant components at 3210 and 3450 cm-1 were assigned to ice-like (for example ES) and disordered (for example CS) [1310]. [Back]
Home | Site Index | Microwave effects | Water molecule | Magnetic effects | Notes | LSBU | Top
This page was last updated by Martin Chaplin on 11 January, 2010